A fair coin is tossed 6 times.
Calculate the probability of obtaining at most three heads.
Student: Mr. C, we learned this under Probability
We did some examples.
Teacher: That is correct.
But remember the examples we did was for four tosses of a fair coin
Student: Yes, we used the Punnett Square
We can also use Tree Diagrams
Teacher: Okay, but using Punnett Square or Tree Diagram to solve 6 tosses of a fair coin will take more time
Student: But, it can still be done...
Teacher: Yes
Student: Can we use it to solve this question?
I understand the Punnett Square better
Teacher: We can...
But this question satisfies the requirements for a Binomial distribution
Let us solve it as a Binomial distribution first
Then, we can solve it using a Punnett Square
First Method:
Binomial Distribution Formulas
$
Fair\;\;coin = 2 \;\;faces = H,\;\;T \\[3ex]
P(H) = p = success = \dfrac{1}{2} \\[5ex]
P(T) = q = failure = 1 - p = 1 - \dfrac{1}{2} = \dfrac{1}{2} \\[5ex]
Tossed\;\;6\;\;times \rightarrow n = 6 \\[3ex]
At\;\;most\;\;3H \implies x = 0H,\;\;x = 1H,\;\;x = 2H,\;\;x = 3H \\[3ex]
P(at\;\;most\;\;3H) = P(x = 0) + P(x = 1) + P(x = 2) + P(x = 3) \\[3ex]
P(x = 0) = C(6, 0) * 0.5^0 * 0.5^{6 - 0} \\[3ex]
C(6, 0) = \dfrac{6!}{(6 - 0)! * 0!} \\[5ex]
= \dfrac{6!}{6! * 1} \\[5ex]
= 1 \\[3ex]
\implies \\[3ex]
P(x = 0) = 1 * 1 * 0.5^6 \\[3ex]
P(x = 0) = 0.015625 \\[3ex]
P(x = 1) = C(6, 1) * 0.5^1 * 0.5^{6 - 1} \\[3ex]
P(x = 1) = C(6, 1) * 0.5^1 * 0.5^5 \\[3ex]
C(6, 1) = \dfrac{6!}{(6 - 1)! * 1!} \\[5ex]
= \dfrac{6 * 5!}{5! * 1} \\[5ex]
= 6 \\[3ex]
\implies \\[3ex]
P(x = 1) = 6 * 0.5 * 0.03125 \\[3ex]
P(x = 1) = 0.09375 \\[3ex]
P(x = 2) = C(6, 2) * 0.5^2 * 0.5^{6 - 2} \\[3ex]
P(x = 2) = C(6, 2) * 0.5^2 * 0.5^4 \\[3ex]
C(6, 2) = \dfrac{6!}{(6 - 2)! * 2!} \\[5ex]
= \dfrac{6 * 5 * 4!}{4! * 2 * 1} \\[5ex]
= 3(5) \\[3ex]
= 15 \\[3ex]
\implies \\[3ex]
P(x = 2) = 15 * 0.25 * 0.0625 \\[3ex]
P(x = 2) = 0.234375 \\[3ex]
P(x = 3) = C(6, 3) * 0.5^3 * 0.5^{6 - 3} \\[3ex]
P(x = 3) = C(6, 3) * 0.5^3 * 0.5^3 \\[3ex]
C(6, 3) = \dfrac{6!}{(6 - 3)! * 3!} \\[5ex]
= \dfrac{6 * 5 * 4 * 3!}{3! * 3 * 2 * 1} \\[5ex]
= 5(4) \\[3ex]
= 20 \\[3ex]
\implies \\[3ex]
P(x = 3) = 20 * 0.125 * 0.125 \\[3ex]
P(x = 3) = 0.3125 \\[3ex]
\therefore P(at\;\;most\;\;3H) \\[3ex]
= P(x = 0) + P(x = 1) + P(x = 2) + P(x = 3) \\[3ex]
= 0.015625 + 0.09375 + 0.234375 + 0.3125 \\[3ex]
= 0.65625 \\[3ex]
$
Second Method:
Punnett Square
6 tosses of a fair coin
6 tosses = 4 tosses + 2 tosses
At most 3 heads = 3 heads or less
This implies: 3 heads, 2 heads, 1 head, and 0 head
These will be in dark blue color
Sample Space for the Six Tosses of 1 Fair Coin
4 tosses in the Column and 2 tosses in the Row
$2\:\:Tosses\:\:\rightarrow$
$4\:\:Tosses\:\:\downarrow$
|
$HH$ |
$HT$ |
$TH$ |
$TT$ |
| $HHHH$ |
$HHHHHH$ |
$HHHHHT$ |
$HHHHTH$ |
$HHHHTT$ |
| $HHHT$ |
$HHHTHH$ |
$HHHTHT$ |
$HHHTTH$ |
$HHHTTT$ |
| $HHTH$ |
$HHTHHH$ |
$HHTHHT$ |
$HHTHTH$ |
$HHTHTT$ |
| $HHTT$ |
$HHTTHH$ |
$HHTTHT$ |
$HHTTTH$ |
$HHTTTT$ |
| $HTHH$ |
$HTHHHH$ |
$HTHHHT$ |
$HTHHTH$ |
$HTHHTT$ |
| $HTHT$ |
$HTHTHH$ |
$HTHTHT$ |
$HTHTTH$ |
$HTHTTT$ |
| $HTTH$ |
$HTTHHH$ |
$HTTHHT$ |
$HTTHTH$ |
$HTTHTT$ |
| $HTTT$ |
$HTTTHH$ |
$HTTTHT$ |
$HTTTTH$ |
$HTTTTT$ |
| $THHH$ |
$THHHHH$ |
$THHHHT$ |
$THHHTH$ |
$THHHTT$ |
| $THHT$ |
$THHTHH$ |
$THHTHT$ |
$THHTTH$ |
$THHTTT$ |
| $THTH$ |
$THTHHH$ |
$THTHHT$ |
$THTHTH$ |
$THTHTT$ |
| $THTT$ |
$THTTHH$ |
$THTTHT$ |
$THTTTH$ |
$THTTTT$ |
| $TTHH$ |
$TTHHHH$ |
$TTHHHT$ |
$TTHHTH$ |
$TTHHTT$ |
| $TTHT$ |
$TTHTHH$ |
$TTHTHT$ |
$TTHTTH$ |
$TTHTTT$ |
| $TTTH$ |
$TTTHHH$ |
$TTTHHT$ |
$TTTHTH$ |
$TTTHTT$ |
| $TTTT$ |
$TTTTHH$ |
$TTTTHT$ |
$TTTTTH$ |
$TTTTTT$ |
$
n(S) = 16 * 4 = 64 \\[3ex]
Let\;\;E = At\;\;most\;\;3H = dark\;blue\;\;color \\[3ex]
n(E) = 42 \\[3ex]
P(E) = \dfrac{n(E)}{n(S)} \\[5ex]
= \dfrac{42}{64} \\[5ex]
= 0.65625 \\[3ex]
$
Third Method:
Binomial Distribution Tables
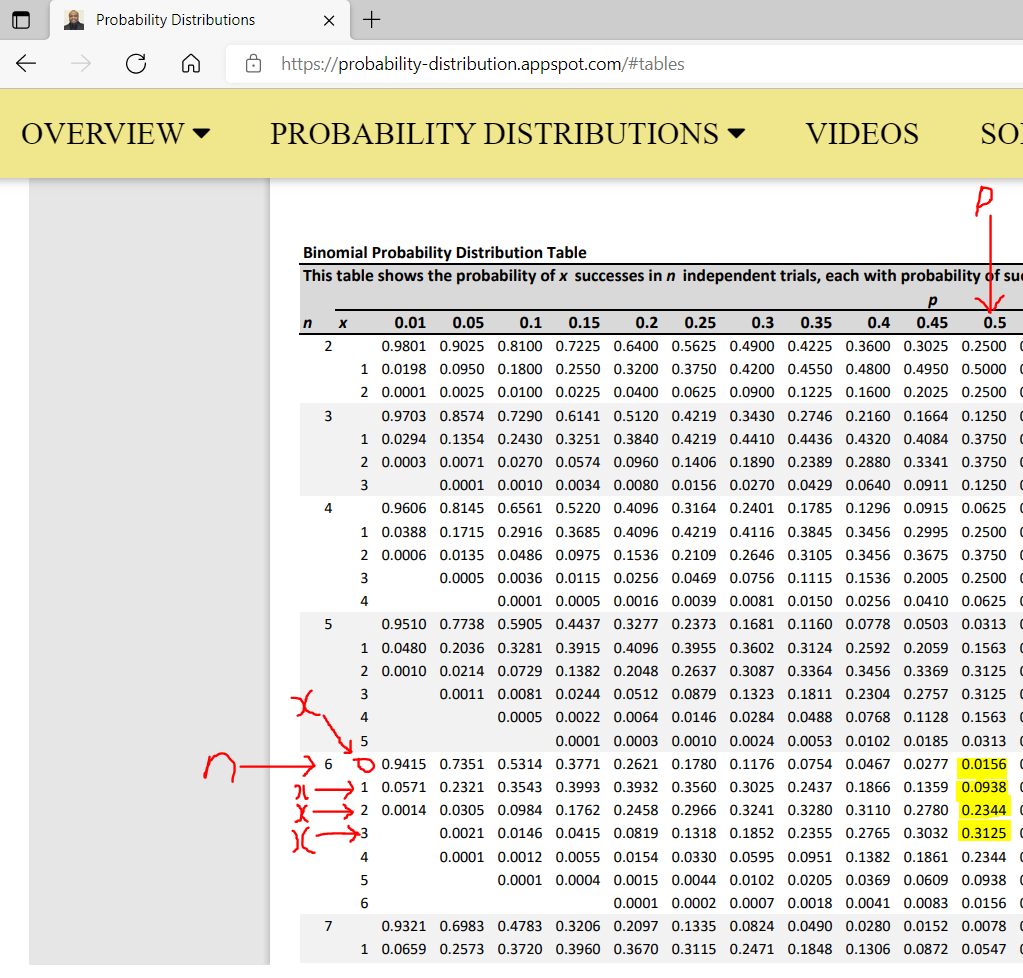
$
P(at\;\;most\;\;3H) \\[3ex]
= P(x = 0) + P(x = 1) + P(x = 2) + P(x = 3) \\[3ex]
P(x = 0) = 0.0156 \\[3ex]
P(x = 1) = 0.0938 \\[3ex]
P(x = 2) = 0.2344 \\[3ex]
P(x = 3) = 0.3125 \\[3ex]
\implies \\[3ex]
P(at\;\;most\;\;3H) \\[3ex]
= 0.0156 + 0.0938 + 0.2344 + 0.3125 \\[3ex]
= 0.6563
$
 Prerequisite Topics
Prerequisite Topics